Pièces
Bondisseurs
Les Bondisseurs réguliers sont des pièces que l’on appelle le plus souvent simplement « Bondisseurs ». On peut les qualifier de réguliers pour souligner qu’ils sont créés en utilisant la règle qui sert à créer le Cavalier classique à partir du Bondisseur simple de coordonnées 1 et 2.
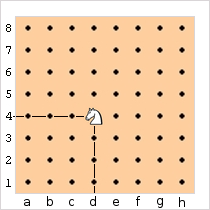
Si, comme au xiangqi (échecs chinois), l’emplacement des pièces sur le plateau de jeu est représenté par des points plutôt que par des cases, on pourra mieux comprendre, en prenant l’exemple du Cavalier, comment on peut définir simplement les Bondisseurs réguliers.
Les coordonnées numériques remplaçant les coordonnées « alphanumériques », le Cavalier « d4 » a pour coordonnées 4 et 4 et peut choisir entre huit cases pour son prochain coup. Ce sont les cases de coordonnées (4+1,4+2), (4+2,4+1), (4-1,4-2), (4-2,4-1), (4+1,4-2), (4+2,4-1), (4-1,4+2), (4-2,4+1). On voit qu’il faut faire varier les coordonnées d’un et deux points de huit façons différentes : on dira que le Cavalier est le Bondisseur-(1,2), l’ordre de ces entiers étant indifférent. Si l’on avait placé le Cavalier au point de coordonnées (0,0), on aurait obtenu les points d’arrivée suivants : (1,2), (2,1), (-1,-2), (-2,-1), (1,-2), (2,-1), (-1,2), (-2,1).
On modifie la valeur absolue de chaque coordonnée du point de départ pour obtenir celles du point d’arrivée de telle manière qui si l’une varie d’une unité, l’autre varie de deux.
Deux nombres (n et m) suffisent pour définir un Bondisseur régulier. De nombreux Bondisseurs réguliers ont reçu un nom (Voir : Tableau), les Bondisseurs anonymes se contentant d’une appellation mathématique.
Remarque
Un Bondisseur régulier vise au plus quatre cases si n est m sont égaux (comme l’Alfil qui est le Bondisseur-(2,2)) ou si une des coordonnées est égale à zéro (comme le Dabbaba qui est le Bondisseur-(0,2)). Dans le premier cas, le Bondisseur est représenté par un dessin de Fou tourné, dans le second par un dessin de Tour tourné.
Ouvrage créé et géré à l'aide de SPIP, logiciel libre distribué sous Licence publique générale GNU (GNU GPL). Origine des images des pièces du jeu d'échecs et des échiquiers (Wikimedia Commons). D’autres informations : e-chekk.