Énoncés
Inverse
Voir aussi le texte introductif de ce chapitre : Inverse.
Dans ce qui suit, le but est le mat du Roi noir. D’autres buts peuvent lui être substitués.
Si le mat est le but du problème, l’énoncé complet d’un problème inverse en n coups est : « Les Blancs jouent et forcent les Noirs à faire mat en n coups au plus » (n est un entier naturel). Le but du problème est donc le mat du Roi blanc. Les Blancs doivent forcer les Noirs à atteindre le but, ces derniers cherchant à l’éviter par tous les moyens. On voit donc que le problème inverse ne se différencie pas du problème direct par les attitudes des camps en présence. Les deux camps ont des attitudes opposées, attitude positive pour les Blancs et attitude négative pour les Noirs. Ce qui différencie les deux genres, c’est que ce sont les Noirs qui atteignent le but dans le problème inverse.
Remarque : Si les Blancs sont forcés de faire mat, la partie se termine et ils échouent. Il y a un but concurrent comme pour un problème direct.
Énoncé et canevas
- ‡n veut dire : direct, mat du Roi noir, en n coups. On peut écrire d‡n, pour être plus explicite.
- s‡n veut dire inverse, mat, en n coups.
Le Canevas de la solution d’un problème inverse en deux coups s’écrit :
1. B1 N1 2. B2 N2 ‡
« B » désignant un coup blanc et « N », un coup noir. Le premier coup est appelé clé. Les coups noirs doivent tous être suivis d’une réponse blanche efficace.
Exemples de problèmes en un coup

- Diagramme A
- s‡1 Les Blancs jouent et forcent les Noirs à faire mat en un coup
Diagramme A : La solution a la forme 1. B1 N1 ‡.
Solution : 1. Cb3† C×b3 ‡. Le coup blanc est un coup d’échec. La seule parade noire fait mat.
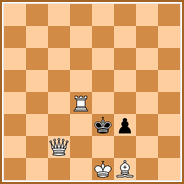
- Diagramme B
- s‡1 Les Blancs jouent et forcent les Noirs à faire mat en un coup
Diagramme B : Les Blancs exploitent l’obligation de jouer (Zugzwang).
Solution : 1. Dd1 f2 ‡

- Diagramme C
- s‡1 Les Blancs jouent et forcent les Noirs à faire mat en un coup
Diagramme C : Les Blancs exploitent encore l’obligation de jouer.
Solution : 1. Fc6 F×c6 ‡
Direct et inverse
Le but le plus courant d’un problème direct est le mat du Roi noir ; le but le plus courant dans un problème inverse sera le mat du Roi blanc. Le nom « inverse » vient de cette inversion des destins des Rois, mais cette inversion n’en fait pas la spécificité. En effet, un problème direct peut avoir le même but qu’un problème inverse (par exemple, obtenir une position comportant un certain nombre de pièces).
Si l’on compare le problème direct au problème inverse, on constate tout d’abord qu’ils ont un point commun : la lutte entre Blancs et Noirs qui existe dans les deux cas. On voit que, dans le problème inverse, l’attitude de chacun des camps vis-à-vis de l’objectif à atteindre ne change pas par rapport au problème « direct ». Les Blancs cherchent à obtenir le mat du Roi blanc contre la volonté des Noirs. Un problème inverse peut même parfaitement être assimilé à un problème direct. Les Blancs jouent et obtiennent une position où les Noirs sont forcés d’atteindre le but en un coup. Cette position est le nouveau but et ce sont les Blancs qui l’atteignent.
On constate donc que ce qui les distingue l’un de l’autre, c’est le fait que ce sont les Blancs qui jouent le dernier coup et atteignent le but dans le problème direct, et les Noirs dans le problème inverse.
En pratique, ce qui différencie vraiment le direct de l’inverse, c’est que les Blancs forcent les Noirs à construire quelque chose. Autrement dit, dans le jeu d’un problème direct dont le but est le mat, les Blancs chassent le Roi noir protégé par les siens ; dans l’inverse, les Blancs domptent les Noirs qui sont forcés d’effectuer une certaine tâche.
On sait qu’il est difficile de faire boire un âne qui n’a pas soif (problème inverse). On n’utilise pas les mêmes stratégies pour l’empêcher de boire (problème direct). Cette difficulté à forcer les Noirs à être constructifs a amené l’invention du problème réflexe, ainsi que l’adoption de règles restreignant le jeu des Noirs (Voir : Maximum).
Voir : Œuvres du genre inverse
Vérification par ordinateur
- Popeye
- WinChloe
Traductions
- Allemand : Selbst(matt)
- Anglais : Self(mate)
Ouvrage créé et géré à l'aide de SPIP, logiciel libre distribué sous Licence publique générale GNU (GNU GPL). Origine des images des pièces du jeu d'échecs et des échiquiers (Wikimedia Commons). D’autres informations : Echekk.